Research - (2021) Volume 0, Issue 0
Amaranth variability at different doses of gamma radiation
O.V. Hudym, S.V. Lymanska, T.I. Goptsiy, N.P. Turchynova, V.O. Mykhailenko, R.V. Kryvoruchenko, R.V. Rozhkov and S.V. Stankevych*Abstract
The article presents the variability in mutant generations of amaranth seed (Amaranthus hópochonacdrius L.) using different doses of gamma radiation. The negative effect of gamma irradiation on amaranth field germination plants of M1 was proved, which decreased with an increase in the mutagen dose (on average, it was 58-50% in the control variant, 49-55, and 2-3% respectively). Plants M1, which grew from seeds treated with mutagen, were characterized by moderate and significant depression of growth processes (a decrease in plant height and panicle length by an average of 10-15 cm compared to the control). Doses of gamma radiation of 400 and 700 Gy induced chlorophyll changes (Albina type), which led to a complete disruption of chlorophyll synthesis in plants. Gamma irradiation has been established to be one of the powerful factors that can significantly change the characteristics of amaranth plants. The changes are manifested in the form of non-hereditary morphoses M1 and mutant plants of M2 and M3 generations. Mutants were isolated in the studied amaranth varieties with increased seed productivity (by weight 1000 and by weight of seeds from a panicle, they exceeded the control by 0.07-0.12 g and 1.11 g, respectively). Mutations in the cultivars studied under the influence of gamma irradiation (150 Gy) can be used as marker traits when mutating amaranth.
https://www.mobafire.com/profile/bodrumboatcharter12-1124493?profilepage https://www.youmagine.com/bodrumboatcharter12/designs https://www.myminifactory.com/users/Bodrumboatcharter12 http://qooh.me/Bodrumboat https://linktr.ee/bodrumboatcharter12 https://pubhtml5.com/homepage/cyfrz/ https://telegra.ph/Bodrumboatcharter12-10-06 https://www.diggerslist.com/65200edb609f8/about https://allmyfaves.com/Bodrumboatcharter12 https://www.metal-archives.com/users/Bodrumboatcharter12 https://www.catchafire.org/profiles/2517778/ https://www.fimfiction.net/user/643612/Bodrumboatcharter12 https://www.hebergementweb.org/members/bodrumboatcharter12.562642/ https://www.sqlservercentral.com/forums/user/bodrumboatcharter12 https://www.twitch.tv/bodrumboatcharter12/about https://www.roleplaygateway.com/member/Bodrumboatcharter12/ https://www.provenexpert.com/bodrumboatcharter12/?mode=preview https://www.intensedebate.com/people/Bodrumboatt https://www.indiegogo.com/individuals/35449325 https://visual.ly/users/bodrumboatcharter/portfolio https://slides.com/bodrumboatcharter12 https://letterboxd.com/bodrumboatchart/ https://fliphtml5.com/dashboard/public-profile/vaszk https://community.windy.com/user/bodrumboat https://speakerdeck.com/bodrumboatcharter12 https://trello.com/u/bodrumboatcharter https://3dwarehouse.sketchup.com/user/de2dd7d0-2dae-4bdd-a23b-ec96ee37b233/Bodrumboatcharter12-B https://www.wattpad.com/user/Bodrumboatcharter12 https://www.goodreads.com/user/show/170494365-bodrumboatcharter12 https://gravatar.com/bodrumboatcharter https://www.mapleprimes.com/users/Bodrumboatcharter12 https://medium.com/@bodrumboatcharter https://www.ted.com/profiles/45231364 https://www.infragistics.com/community/members/1d7b0f7c364bf6536b4d8cf41f511023169b4d97?_ga=2.172971107.1358979024.1696603040-536746857.1696603039 https://www.metooo.io/u/65201c0779c47c11a2ee00af https://app.roll20.net/users/12503762/bodrumboatcharter12-b https://list.ly/bodrumboatcharter/activity https://giphy.com/channel/Bodrumboatcharter12 https://www.tumblr.com/bodrumboatcharter12 https://www.creativelive.com/student/bodrumboatcharter12?via=accounts-freeform_2 https://gab.com/Bodrumboatcharter12 https://www.flickr.com/people/199265856@N05/ https://seedandspark.com/user/bodrumboatcharter12-01hc4gehwfv7jsg1p5qm2n7nv8 https://os.mbed.com/users/bodrumboatcharter12/ https://calis.delfi.lv/blogs/lietotajs/317997-bodrumboatcharter12/ https://notionpress.com/author/933773 https://my.desktopnexus.com/Bodrumboatcharter12/ https://guides.co/a/bodrumboatcharter12-bodrumboatcharter12/ https://www.bahamaslocal.com/userprofile/1/250186/Bodrumboatcharter12.html http://molbiol.ru/forums/index.php?showuser=1302342 https://www.credly.com/users/bodrumboatcharter12-bodrumboatcharter12/badges https://ko-fi.com/bodrumboatcharter12#paypalModal https://devpost.com/bodrumboatcharter?ref_content=user-portfolio&ref_feature=portfolio&ref_medium=global-nav https://www.redbubble.com/people/Bodrumboat/shop?asc=u https://hub.docker.com/u/bodrumboatcharter12 http://onlineboxing.net/jforum/user/editDone/254299.page https://micro.blog/Bodrumboatcharter12 http://www.effecthub.com/user/3729559 http://hawkee.com/profile/5140816/ https://wefunder.com/bodrumboatcharter12 https://www.facer.io/user/axSXKCcsqA https://mastodon.online/@Bodrumboatcharter12 https://sketchfab.com/Bodrumboatcharter12 https://profiles.wordpress.org/bodrumboatcharter12/ https://dzone.com/users/5004481/bodrumboatcharter12.html https://www.mobafire.com/profile/bluecruiseturkey12-1124220?profilepage http://hawkee.com/profile/5120349/ https://www.youmagine.com/bluecruiseturkey12/designs https://www.myminifactory.com/users/Bluecruiseturkey12 http://qooh.me/Bluecruise https://linktr.ee/bluecruiseturkey12 https://pubhtml5.com/homepage/djvpw/ https://telegra.ph/Bluecruiseturkey12-10-04 https://www.diggerslist.com/651d2ecfdf065/about https://allmyfaves.com/Bluecruiseturkey12 https://www.metal-archives.com/users/Bluecruiseturkey12 [[[[[[[[[[[[[mail bekleniyor daha gelmedi sabah kontrol et]] https://www.catchafire.org/profiles/2514952/ https://www.fimfiction.net/user/642755/Bluecruiseturkey12 https://www.hebergementweb.org/members/bluecruiseturkey12.561596/ https://www.sqlservercentral.com/forums/user/bluecruiseturkey12 https://www.twitch.tv/bluecruiseturkey12/about https://www.roleplaygateway.com/member/Bluecruiseturkey12/ https://www.provenexpert.com/bluecruiseturkey12/?mode=preview https://www.intensedebate.com/people/Bluecru https://www.indiegogo.com/individuals/35422352 https://visual.ly/users/bluecruiseturkey/portfolio https://slides.com/bluecruiseturkey12 https://letterboxd.com/bluecruiseturke/ https://fliphtml5.com/dashboard/public-profile/llxdj https://community.windy.com/user/bluecruise https://speakerdeck.com/bluecruiseturkey12 https://trello.com/u/bluecruiseturkey https://3dwarehouse.sketchup.com/user/38b61a87-73b5-4478-84b6-6ed07331ab65/Bluecruiseturkey12-B https://www.wattpad.com/user/Bluecruiseturkey12 https://www.goodreads.com/user/show/170435355-bluecruiseturkey12 https://gravatar.com/bluecruiseturkeyf80ec2ddfb https://tr.pinterest.com/maviyolculukonline/ https://www.mapleprimes.com/users/Bluecruiseturkey12 https://medium.com/@bluecruiseturkey https://www.ted.com/profiles/45212773 https://www.infragistics.com/community/members/0be9390112c7a0030a5d74f39491a84152b988cf?_ga=2.60931624.541346193.1696417729-65453483.1696417729 https://www.metooo.io/u/651d485866133011a1e7753b https://app.roll20.net/users/12496298/bluecruiseturkey12-b https://list.ly/bluecruiseturkey/activity https://giphy.com/channel/Bluecruiseturkey12 https://www.tumblr.com/bluecruiseturkey12 https://www.creativelive.com/student/bluecruiseturkey12?via=accounts-freeform_2 https://gab.com/Bluecruiseturkey12 https://sketchfab.com/Bluecruiseturkey12 https://www.flickr.com/people/199265875@N03/ https://profiles.wordpress.org/bluecruiseturkey12/ https://wefunder.com/bluecruiseturkey12 https://seedandspark.com/user/bluecruiseturkey12-01hbx6zr7fag2jqjemqctz46xj https://calis.delfi.lv/blogs/posts/214915-httpsbluecruiseturkeyco/lietotajs/317499-bluecruiseturkey12/ https://os.mbed.com/users/bluecruiseturkey12/ https://notionpress.com/author/932684 https://my.desktopnexus.com/Bluecruiseturkey12/ https://guides.co/a/bluecruiseturkey12-bluecruiseturkey12/ https://www.bahamaslocal.com/userprofile/1/249117/Bluecruiseturkey12.html http://molbiol.ru/forums/index.php?showuser=1301780 https://www.credly.com/users/bluecruiseturkey12-bluecruiseturkey12/badges https://www.facer.io/user/9OSgH8lLUu https://ko-fi.com/bluecruiseturkey12#paypalModal https://mastodon.online/@Bluecruiseturkey12 https://devpost.com/bluecruiseturkey?ref_content=user-portfolio&ref_feature=portfolio&ref_medium=global-nav https://www.redbubble.com/people/Bluecruis/shop?anchor=profile&asc=u https://dzone.com/users/5003084/bluecruiseturkey12.html https://hub.docker.com/u/bluecruiseturkey12 http://onlineboxing.net/jforum/user/editDone/253923.page http://www.effecthub.com/user/3729187 https://micro.blog/Maviyolculukonline12 https://www.mobafire.com/profile/besthairtransplant12-1123844?profilepage https://www.youmagine.com/besthairtransplant12/designs https://www.myminifactory.com/users/Besthairtransplant12 http://qooh.me/Besthairt https://linktr.ee/besthairtransplant12 https://pubhtml5.com/homepage/gqmff/ https://telegra.ph/Besthairtransplant12-10-02 https://www.diggerslist.com/651a812418cea/about https://allmyfaves.com/Besthairtransplant12 https://www.metal-archives.com/users/Besthairtransplant12 https://www.catchafire.org/profiles/2513167/ https://www.fimfiction.net/user/642086/Besthairtransplant12 https://www.hebergementweb.org/members/besthairtransplant12.560830/ https://www.sqlservercentral.com/forums/user/besthairtransplant12 https://www.twitch.tv/besthairtransplant12/about https://www.roleplaygateway.com/member/Besthairtransplant12/ https://www.provenexpert.com/besthairtransplant12/?mode=preview https://www.intensedebate.com/people/Besthair12 https://www.indiegogo.com/individuals/35400980 https://visual.ly/users/besthairtransplant12/portfolio https://slides.com/besthairtransplant12 https://letterboxd.com/besthairr/ https://fliphtml5.com/dashboard/public-profile/imjqe https://community.windy.com/user/besthairtransp https://speakerdeck.com/besthairtransplant12 https://trello.com/u/besthairtransplant12 https://3dwarehouse.sketchup.com/user/aae1c26c-a3d5-45eb-9627-c0853a860d3b/Besthairtransplant12-B https://www.wattpad.com/user/Besthairtransplant12 https://www.goodreads.com/user/show/170382750-besthairtransplant12 https://gravatar.com/besthairtransplant12 https://tr.pinterest.com/besthairtransplant12/ https://www.mapleprimes.com/users/Besthairtransplant12 https://medium.com/@besthairtransplant12 https://www.ted.com/profiles/45197096 https://www.infragistics.com/community/members/adcd427ea388c1629996582e13d2b0a2c25ca61c?_ga=2.200070894.113000698.1696261445-1288411814.1696261445 https://www.metooo.io/u/651ae70566133011a1e604fc https://app.roll20.net/users/12490052/besthairtransplant12-b https://list.ly/besthairtransplant12/activity https://giphy.com/channel/Besthairtransplant12 https://www.tumblr.com/besthairtransplant12 https://www.creativelive.com/student/besthairtransplant12?via=accounts-freeform_2 https://gab.com/Besthairtransplant12 https://www.flickr.com/people/199263168@N04/ https://seedandspark.com/user/besthairtransplant12-01hbt6wnfb7k9h9bt6pfjbjzsp https://os.mbed.com/users/besthairtransplant12/ https://calis.delfi.lv/blogs/posts/214781-httpsbesthairtransplantco/lietotajs/317265-besthairtransplant12/ https://notionpress.com/author/932148 https://my.desktopnexus.com/Besthairtransplant12/ https://guides.co/a/besthairtransplant12-besthairtransplant12/ https://www.bahamaslocal.com/userprofile/1/248608/Besthairtransplant12.html http://molbiol.ru/forums/index.php?showuser=1301548 https://www.credly.com/users/besthairtransplant12-besthairtransplant12/badges https://ko-fi.com/besthairtransplant12#paypalModal https://devpost.com/hairclinicistanbul?ref_content=user-portfolio&ref_feature=portfolio&ref_medium=global-nav https://www.redbubble.com/people/Hairclinicc/shop?asc=u https://hub.docker.com/u/besthairtransplant12 http://onlineboxing.net/jforum/user/edit/253721.page https://micro.blog/Besthairtransplant12 http://www.effecthub.com/user/3729017 http://hawkee.com/profile/5094365/ https://wefunder.com/besthairtransplant12 https://www.facer.io/user/IBoUwjxbMK https://mastodon.online/@Hairclinicistanbul12 https://sketchfab.com/Hairclinicistanbul12 https://profiles.wordpress.org/hairclinicistanbul12/ https://dzone.com/users/4999725/besthairtransplant12.html
Keywords
Amaranth, Mutagenesis, Gamma irradiation, Morphosis, Variability.
Introduction
Mutations are the primary material for the natural selection and evolution of species. The mutational process saturates populations with numerous changes, because of which such populations carry vast reserves of latent hereditary variability and maintain the plasticity of the species, adaptability to unfavorable environmental conditions. A. Nadson and G. S. Filippov carried out the first successful attempt to use radiation to obtain mutations in 1925 in fungi (Vasko et al., 2015; Nadson, 1920). However, the genetics of fungi (yeast) was not studied at all, so the authors could not prove that the selection of forms they made is based on the induction of hereditary mutations. World practice shows that most mutant varieties are created using physical mutagens (Vasko et al., 2015; Vasilkivsky et al., 2012; Kozachenko, 2010). The most convincing mutagenic effect of X-ray radiation was demonstrated by G. Möller (1926) using the example of Drosophila, L. Stadler (1928) on barley and corn, L. Delone (1957), and A. A. Sapegin (1925)-on wheat. However, radiation selection began to develop only after available radiation sources (mainly X-rays, γ-radiation) appeared.
However, the lack of sufficient information on the effect of gamma irradiation on the variability of traits in amaranth mutant generations now remains insufficiently studied (Goptsiy, 1999; Kapravius, 1997; Gupta, 1996; Greizerstein, 1992). Therefore, the aim was to study the effect of gamma radiation optimally doze on the genetic effects after exposure to a mutagen on amaranth seeds.
Materials and Methods
The experiments were carried out on the experimental fields of the V.V. Dokuchaev Kharkiv National Agrarian University in 2016 2018 2020. The starting material was three varieties of the amaranth A. hupochondriacus: Sam (AS No. 1474, 2001), Kharkiv-1, Student (AS No. 03157, 2003). The seeds were exposed to gamma radiation. Source-Co60. Doses: 15, 30, 40, 150, 400, and 700 Gy. Place of processing-NSC Institute of Metrology. Installation-DETU 12-05-02. Irradiation conditions: ambient air temperature-12-13°, relative air humidity-82%, atmospheric pressure-994 hPa, volumetric heterogeneity of the absorbed dose in the sample no more than ± 15%, absorbed dose rate 0.2-0.5 kGy/h, the method of irradiation is continuous under conditions of free penetration of air into the irradiated sample from all sides. As a control, we used dry seeds of amaranth varieties Student, Kharkiv-1, and Sam without treatment.
Each variant of the irradiated seeds was seeded in separate rows 1 m long, 10 rows per plot. In each variant M1, 100 plants were self-pollinated. The seeds collected from the self-pollinated plants were sown individually in single-row plots, 20 plants per row. In each family of M2, three to five plants were self-pollinated. The seeds of the self-pollinated plants were seeded in separate rows, 20 plants per row. Only morphologically altered plants were self-pollinated in the M3 family. Sowing was carried out manually at the optimal time (second or third decade of May); the predecessor was winter wheat. The collection of mutant plants in the experimental plots was carried out by cutting and threshing by hand threshing into separate bags (Kozachenko, 2010; Goptsiy, 1999). We used the classification of mutations proposed by V.V. Morgun and V.F. Logvinenko (Morgun, 1995).
We studied the nature of the variability of quantitative (mass of seeds per panicle, the mass of 1000 seeds), biometric (plant height, panicle length), morphological (change in color of panicle, seeds, leaf shape) characteristics of amaranth varieties during the growing season. Observation, registration, and biometric measurements were carried out according to the "Methodology for the examination of amaranth varieties (Amaranthus L.) for difference, uniformity, and stability" (International Union for the protection of new varieties of plants, 2008), the weight of seeds from one panicle and the weight of 1000 seeds was determined according to the State Standard GOST 2949-94 (Agricultural seeds, 1996).
Results
Features of the growth and development of amaranth varieties under gamma irradiation influence in M1 M3.
The main most reliable criteria for plant sensitivity to mutagenic action are laboratory and field germination of seeds, plant survival, and the degree of inhibition of the growth of seedlings and adult plants. On amaranth varieties of A. hupohondriacus Student, Kharkiv-1, Sam, a decrease in field germination and plant survival in M1 was found, which occurred under the influence of gamma rays as a result of an increase in radiation dose. Field germination averaged in the control variant 50-58%, under the influence of a dose of 15 Gy 49-55%, 400 Gy 2-3% depending on the variety. The plant survival rate on average for the variants was 75-78% (15 Gy), 50-55% (150 Gy), compared to the control-78-80% (Fig. 1) (Gudym, 2014).
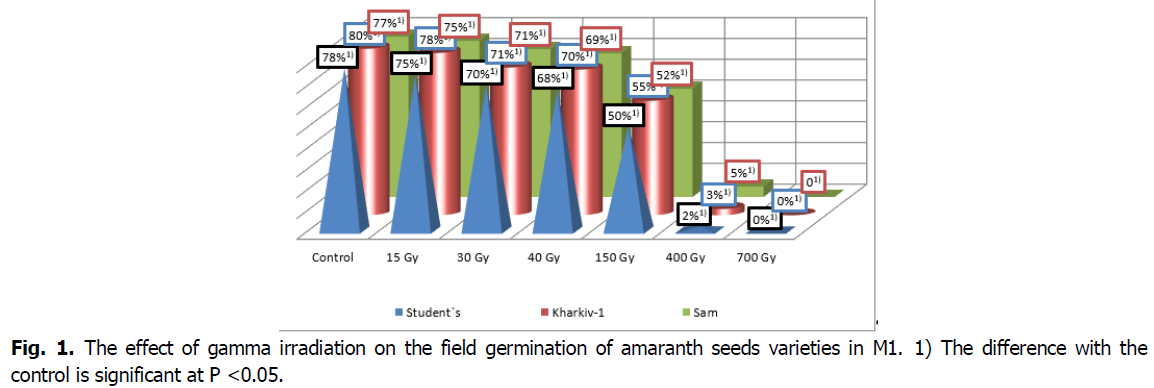
Fig 1. The effect of gamma irradiation on the field germination of amaranth seeds varieties in M1. 1) The difference with the control is significant at P <0.05.
The M1 plants obtained from the seeds treated with mutagens were characterized by a moderate and significant depression of the growth processes. The height of the plants in the treatment options decreased on average of 10-14 cm, the length of the panicle by 15 cm, and the weight of seeds per panicle by 1 to 3 g compared to the control, depending on the variety.
The growth and development of second-generation plants were characterized by a reduction in quantitative traits due to exposure to gamma radiation. Plant height in M2 was lower in all variants of mutagen treatment as compared to the control. Student variety in the variant without treatment (control) was 155 cm and at a dose of 150 g-145 cm. In the Kharkiv-1 and Sam, the plant decreased by 5-13 cm, increasing the radiation dose, respectively (Table 1). The growth and development of plants M3, as well as M1 and M2, was characterized by depression of the traits studied traits because of exposure to gamma radiation.
| Mut. generation | Variant | Student | Kharkiv-1 | Sam | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Plant height сm | Panicle length, сm | Seed's weight, g | Weight 1000 seeds, g | Plant height, сm | Panicle length, сm | Seed's weight, g | Weight 1000 seeds, g | Plant height, сm | Panicle length, сm | Seed's weight, g | Weight 1000 seeds, g | |||||
| М1 | Control | 145 | 30 | 4 | 0.81 | 143 | 35 | 5 | 0.83 | 142 | 33 | 4.5 | 0.79 | |||
| 15 Gy | 142 | 27 | 3.5 | 0.8 | 141 | 31 | 4.5 | 0.81 | 138 | 30 | 3.7 | 0.77 | ||||
| 30 Gy. | 140 | 25 | 3.8 | 0.74 | 138 | 28 | 3.5 | 0.76 | 136 | 29 | 3.4 | 0.72 | ||||
| 40 Gy | 138 | 22 | 3 | 0.72 | 136 | 25 | 3 | 0.74 | 132 | 25 | 2.8 | 0.71 | ||||
| 150 Gy | 135 | 19 | 2.4 | 0.7 | 130 | 21 | 2.5 | 0.71 | 128 | 22 | 2.5 | 0.67 | ||||
| V ± Sv,% | 2.2 ± 0.4 | 9.8 ± 1.3 | 11.5 ± 1.5 | 15.9 ± 1.1 | 2.5 ± 1.1 | 11.8 ± 1.5 | 22.3 ± 1.6 | 15.8 ± 1.1 | 2.8 ± 1.0 | 12.1 ± 1.2 | 14.8 ± 1.0 | 16.5 ± 1.2 | ||||
| М2 | Control | 155 | 40 | 4.5 | 0.81 | 153 | 45 | 5 | 0.83 | 152 | 43 | 5.5 | 0.8 | |||
| 15 Gy | 152 | 37 | 4.3 | 0.8 | 151 | 41 | 4.5 | 0.81 | 148 | 40 | 4.7 | 0.78 | ||||
| 30 Gy. | 150 | 35 | 4 | 0.74 | 148 | 38 | 3.5 | 0.76 | 146 | 39 | 4.4 | 0.74 | ||||
| 40 Gy | 148 | 32 | 3.5 | 0.71 | 146 | 35 | 3 | 0.74 | 142 | 35 | 3.5 | 0.71 | ||||
| 150 Gy | 145 | 29 | 3 | 0.7 | 140 | 31 | 2.5 | 0.71 | 138 | 32 | 3.1 | 0.69 | ||||
| V ± Sv,% | 4.8 ± 1.0 | 14.8 ± 1.2 | 18.5 ± 1.3 | 16.8 ± 1.0 | 4.5 ± 1.2 | 13.6 ± 1.6 | 21.3 ± 1.4 | 16.3 ± 1.2 | 4.7 ± 1.0 | 12.8 ± 1.1 | 13.5 ± 0.9 | 16.8 ± 1.2 | ||||
| М3 | Control | 175 | 50 | 5.5 | 0.82 | 173 | 55 | 6 | 0.85 | 172 | 53 | 6.5 | 0.83 | |||
| 15 Gy | 172 | 47 | 5.3 | 0.8 | 171 | 51 | 5.5 | 0.82 | 168 | 50 | 5.7 | 0.8 | ||||
| 30 Gy. | 170 | 45 | 5 | 0.75 | 168 | 48 | 4.5 | 0.78 | 166 | 49 | 5.4 | 0.76 | ||||
| 40 Gy | 168 | 42 | 4.5 | 0.72 | 166 | 45 | 4 | 0.75 | 162 | 45 | 4.5 | 0.73 | ||||
| 150 Gy | 165 | 39 | 4 | 0.7 | 160 | 41 | 3.5 | 0.71 | 158 | 42 | 4.1 | 0.69 | ||||
| V ± Sv,% | 4.2 ± 0.8 | 9.5 ± 1.2 | 11.8 ± 0.9 | 13.4 ± 0.9 | 4.9 ± 0.7 | 9.9 ± 1.5 | 14.4 ± 1.0 | 18.1 ± 1.1 | 4.1 ± 1.1 | 19.3 ± 1.4 | 13.7 ± 0.9 | 12.5 ± 0.9 | ||||
Table 1. The effect of gamma irradiation on the change in biometric parameters in amaranth plants in M1-M3
The effect of gamma irradiation on the phenotypic variability of traits in amaranth varieties in M1-M3.
As a result of irradiation in the generation of morphoses were obtained, associated with changes in the morphology of amaranth plants (Fig. 2). The morphological changes identified in the mutant generations of amaranth plants were divided into three groups: chlorophyll, morphological, and economically valuable. Each of these types was induced by specific doses of radiation. The highest percentage of chlorophyll changes (84-92%) was manifested under the influence of 400 and 700 Gy; morphological changes were induced by lower doses of radiation (30, 40, 150 Gy) and were in the range of 3.8-20.0%, depending on the variety. Changes in economically valuable traits occurred under the influence of doses of 15 and 150 Gy and varied between 3.3 and 9.0% depending on the variety (Gudym, 2015).

Fig 2. Types of morphoses identified in the studied amaranth varieties amaranth under the influence of gamma irradiation in M1: 1) Branching of the main stem at the bottom; 2) Bifurcation of the panicle; 3) Fasciation of the panicle; 4) Change of color of the panicle; 5) Branching of the main stem in the upper part; 6) Branching of the panicle; 7, 8) Change of the shape of the panicle.
Doses of gamma radiation of 400 and 700 Gy induced chlorophyll changes (Albina type), which led to a complete disruption of chlorophyll synthesis in plants. The highest number of plants with chlorophyll changes was obtained after treatment with a dose of 700 Gy, 87% for Student's variety, 92% for Kharkiv-1 variety, and 90% for Sam variety (Table 2).
| Variant | Variety | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Student | Krarkiv-1 | Sam | |||||||||||||||||||
| Control | 15 Gy | 30 Gy | 40 Gy | 150 Gy | 400 Gy | 700 Gy | Control | 15 Gy | 30 Gy | 40 Gy | 150 Gy | 400 Gy | 700 Gy | Control | 15 Gy | 30 Gy | 40 Gy | 150 Gy | 400 Gy | 700 Gy | |
| Total frequency of modified plants, % | 0.6 | 5.0 1) | 5.8 1) | 11.8 1) | 30.5 1) | 54.0 1) | 87.0 1) | 0.3 | 2.3 | 6.2 1) | 17.2 1) | 35.0 1) | 59.0 1) | 92.0 1) | 0.6 | 2.9 | 7.6 1) | 16.2 1) | 41.7 1) | 58 1) | 90 1) |
| LSD05 | 4.3 | 5 | 4.9 | ||||||||||||||||||
| Chlorophyll, % | - | - | 2.0 | 5.0 1) | 8.0 1) | 54.0 1) | 87.0 1) | - | - | 1.0 | 7.0 1) | 10.0 1) | 59.0 1) | 92.0 1) | - | - | 2.0 | 8.0 1) | 12.0 1) | 58.0 1) | 90,0 1) |
| LSD05 | 2.3 | 2.4 | 2.3 | ||||||||||||||||||
| Morphological, % | 0.3 | 2.0 1) | 3.8 1) | 6.8 1) | 17.5 1) | - | - | 0.3 | 2.3 1) | 5.2 1) | 7.5 1) | 19.0 1) | - | - | 0.6 | 2.9 1) | 5.6 1) | 8.8 1) | 20.0 1) | - | - |
| LSD05 | 1.6 | 1.7 | 1.7 | ||||||||||||||||||
| Economically valuable, % | 0.3 | 3.3 1) | - | - | 5.0 1) | - | - | - | - | - | 2.7 1) | 6.0 1) | - | - | - | - | - | - | 9.7 1) | - | - |
| LSD05 | 0.9 | 0.9 | 0.9 | ||||||||||||||||||
Table 2. The total frequency of the main types of altered plants induced by gamma radiation in M1.
Changes in the M2 morphology of roots, stems, leaves, panicles, seeds, as well as changes in vegetation lines, were observed. The selected changes were found in the amaranth varieties with different frequencies depending on the variety and radiation dose. Changes were observed in the student variety's mutational populations: stems in 6.3-7.7% of plants at a dose of 150 Gy, panicles in 1.6% at 40 Gy, and 5.0% at 150 Gy; seeds in 4.0% at 150 Gy. 3.3% of plants in the treatment variant with a dose of 15 Gy turned out to be maturing earlier. In mutant populations of the Kharkiv-1 variety, the following changes were observed: stems in 7.0-9.0% at a dose of 150 Gy, panicles in 2.3-6.0% under the influence of a dose of 150 Gy, leaves in 5.0% of plants at a dose of 150 gr. Changes were identified in mutant populations of the Sam variety: stems in 9.0% in the variant of treatment with a dose of 150 Gy, panicles in 3.6-8.3% at 150 Gy, seeds in 4.0% at 150 Gy (Table 3).
| Groups of changes in plants | Variety | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Student | Krarkiv-1 | Sam | |||||||||||||
| Control | 15 Gy | 30 Gy | 40 Gy | 150 Gy | Control | 15 Gy | 30 Gy | 40 Gy | 150 Gy | Control | 15 Gy | 30 Gy | 40 Gy | 150 Gy | |
| Stem changes, % | 0.3 | 1.3 | 2.8 | 3.4 | 10.5 | 0.3 | 1.0 | 3.5 | 4.3 | 10.7 | - | 1.3 | 3.0 | 3.4 | 12.0 |
| Leaf changes, % | - | - | - | - | - | - | - | - | - | 5.0 | - | - | - | - | - |
| Panicle changes, % | 0.3 | 0.3 | 3.8 | 4.6 | 11.3 | - | - | - | 3.5 | 11.0 | - | - | - | 3.7 | 11.5 |
| Seeds changes, % | - | - | - | 0.7 | 3.0 | - | - | - | - | - | - | - | - | 0.6 | 3.3 |
| Physiological changes (early maturity), % | - | 3.3 | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 0.3 | 1.3 | 1.2 | 1.2 | 3.2 | 0.3 | 1.0 | 1.2 | 1.5 | 4.45 | 0.0 | 0.65 | 1.4 | 1.58 | 4.51 | |
| S | 0.05 | 0.25 | 0.23 | 0.22 | 0.49 | 0.01 | 0.18 | 0.26 | 0.3 | 0.76 | 0.0 | 0.09 | 0.15 | 0.36 | 0.62 |
| V, % | 16.7 | 48.4 | 53.8 | 59.5 | 62.9 | 10.2 | 18.6 | 22.7 | 26.1 | 76.1 | 0.0 | 33.1 | 33.5 | 33.8 | 55.4 |
Table 3. Groups of plant changes induced by gamma irradiation in amaranth varieties in M2
All M3 varieties showed the same morphological mutations as in M2, but there were fewer of them in M3, especially changes in the root and stem. Analysis of the spectrum and frequency of mutations in M3 plants showed a decrease in the number of altered plant groups and their number in mutant populations. Thus, in the Student variety in M2 in the variant with a dose of 150 Gy, plants with a change in panicle color were 5.0%, while in M3 they were in 3.3% of plants, the number of plants with seed mutations decreased by 2% (from 4 to 2%). Physiological mutations were identified 1.0-3.0% (with 1.7-3.3% in M2) (Fig. 3) (Gudym et al., 2016).
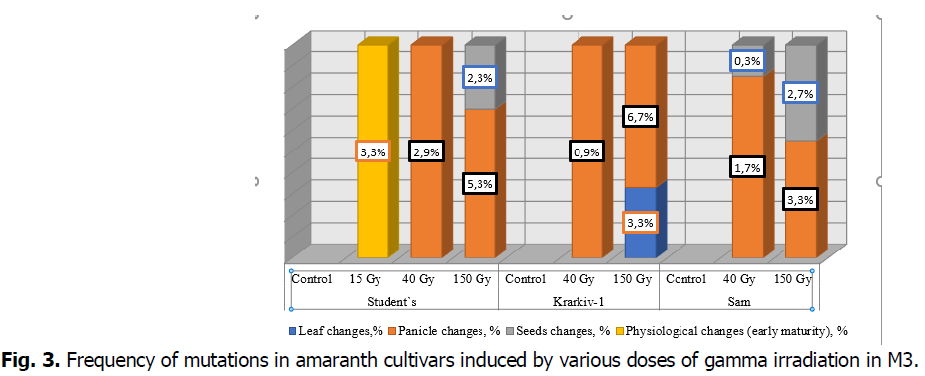
Fig 3. Frequency of mutations in amaranth cultivars induced by various doses of gamma irradiation in M3.
Mutants induced by the 150 Gy irradiation dose of 150 Gy were characterized by an increase in quantitative traits indices in the studied cultivars under the influence of gamma irradiation. In particular, in the Student variety, three plants were identified: two with an increased weight of 1000 seeds (0.89 g, 0.95 g), one with an increased weight of seeds from one panicle (7.15 g), which exceeded the control by 0.07, 0.13, and 1.11 g, respectively. In the Kharkiv-1 variety, two plants were isolated that exceeded the control: one by the weight of 1000 seeds (by 0.04 g) and one by the length of the panicle (by 5 cm). In the Sam variety, three plants were identified: one exceeded the control in plant height (by 8 cm), one in panicle length (by 12 cm), and one plant with an increased weight of 1000 seeds (by 0.12 g) compared to the control (Fig. 4).
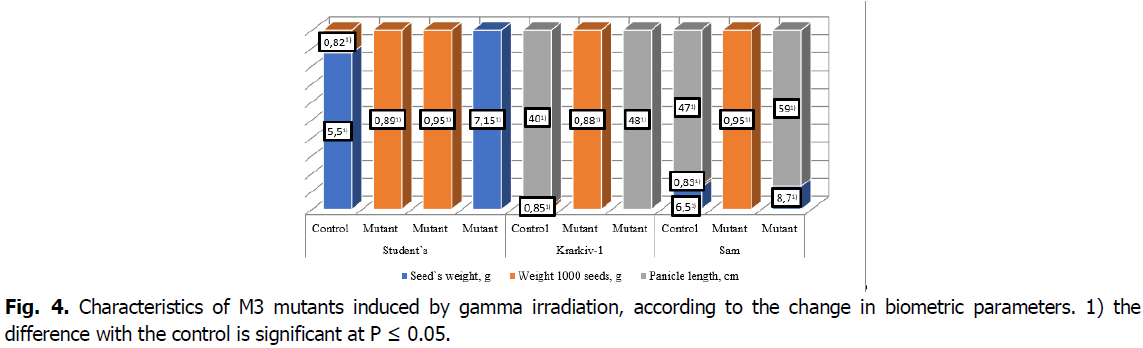
Fig 4. Characteristics of M3 mutants induced by gamma irradiation, according to the change in biometric parameters. 1) the difference with the control is significant at P ≤ 0.05.
Furthermore, mutations were isolated in the studied varieties under the influence of gamma irradiation, which can be used as marker traits. In particular, the Student variety has a red panicle color, the Kharkiv-1 variety has corrugated leaves and pink panicle tips, and the Sam variety has a pink panicle color.
Based on the studies carried out, mutant lines were isolated, which are a valuable starting material for amaranth breeding. Three forms from the Student variety were selected: one was an early maturing form induced by a dose of 15 Gy, and two from the action of a dose of 150 Gy-one with a red panicle, the other with black seeds. In the Kharkiv-1 variety, mutations were identified when treated with a dose of 150 Gy: a corrugated leaf shape and a pink panicle. In the Sam variety, a dose of 150 Gy contributed to the formation of the following changes: black seeds, a green panicle. The created mutant forms were transferred to the National Center for Plant Genetic Resources of Ukraine and can be used in the breeding process.
Discussion
According to T. I. Goptsiy, in the case of gamma-ray treatment, as found in A. hybridus (15 kR), the convergence was expected, and, in terms of similarity, the research variants even exceeded the control ones. However, after a week, the situation of irradiation led to a significant death of externally typical plants (Goptsiy, 1999). According to V.V. Kapraviy, depression in the growth of amaranth plants is directly related to gamma irradiation. The stronger the depression in the growth of plants, the more they die. A twofold decrease in M1 plants' height compared to the control increases their death by the same amount (Kapraviy, 1997).
Studies of the variability of morphological traits carried out by Hauptli and Jain have shown that grain amaranth species harvested from their centers of origin (South and Central America) are characterized by a relatively high degree of homozygosity (Hauptli and Jain, 1980; 1984). T.I. Goptsiy and A.N. Krivoruchenko found that irradiation at a dose of 30 kR given A. hybridus reduced the length of the roots compared to the control by 3.0 and 1.7 times. In the variants with the usage of gamma radiation at doses of 30 and 40 Kp in A. hybridus plants under field conditions, the development of the taproot stopped, the root became thicker, and the plant began to spread (Goptsiy, Krivoruchenko, 2003).
Through the usage of mutagenesis, V. P. Holovin and B. A. Nedilko (1995) received one mutation (compact brush) in the Donetskii variety, a tall mutation in the amaranth salad line, and a mutation in the caudate amaranth, based on which the amaranth medical and food directional variety Herculesik was created. T.I. Goptsiy and the staff of Genetics, Breeding and Seed Production Department, V.V. Dokuchaev Kharkiv National Agrarian University, using mutagenesis, created the Ultra variety, which is characterized by ideal evenness, the short stature of 90-95 cm, early maturity (the length of the growing season is 90-95 days) (Goptsiy et al., 2018).
Conclusion
In summary of the results of our studies, the optimal mutagenic dose of seed treatment was determined in A. hypochondriacus amaranth varieties in 150 Gy, which promoted the expansion of the spectrum and frequency of induced mutational variability and the production of lines with valuable characteristics in terms of breeding. The phenotypic variability of amaranth varieties has been proven, and mutations have been obtained under the influence of gamma radiation, which can be used as marker signs when breeding this culture.
Mutant lines with an increased weight of 1000 seeds and a weight of seeds from one panicle were isolated, which constitute a valuable starting material for breeding. The expediency of using radiation mutagenesis in amaranth to obtain mutants with altered parameters of valuable economic traits necessary to expand the spectrum of the initial material in the breeding of this culture has been substantiated.
References
Delone, L.N. (1957). O metode radiatsionnoy selektsii. Selektsiya i semenovodstvo, 4:23–27 (in Russian).
Goptsiy, T.I., Vornkov, M.F., Horbenko N.I. (1997). Sort amarantu Kharkivskii. No. 97099001 from 28.03.1997 (in Ukrainian).
Goptsiy, T.I. (1999). Amarant: biolohiia, vyroshchuvannia, perspektyvy vykorystannia, selektsiia: Monohrafiia. Kharkiv: KhDAU. (in Ukrainian).
Goptsiy, T.I., Kryvoruchenko, O.M., Voronkov, M.F. (2001). Sort shchyrytsi sem. No 03157, applications No 02099001. (in Ukrainian).
Goptsiy, T.I., Kryvoruchenko, O.M. (2003). Eksperymentalnyi mutahenez u amaranta. Trudy po fundamentalnoi y prykladnoi henetyke. Kharkiv, 2:217-230 (in Ukrainian).
Goptsiy, T.I. (2018). Amarant: selektsiia, henetyka ta perspektyvy vyroshchuvannia: Monohrafiia. Kharkiv: KhNAU (in Ukrainian).
Greizerstein, E.J., Poggio, L. (1992). Estudios atogeneticos de seis hybridos interspecificos de Amaranthus (Amaranthaceae). Darwiniana, 311:159-165.
Gupta, C., Dobos, G., Gretmacher, C. (1996). Comparosin from the grain amaranth species A. cruentus and A. hypochendriacus. Proceed. Symp. on breeding of oil and protein crops. Kyiv.
Hauptli, H., Jain, K. (1980). Genetic polymorphisms and components in a population of amaranth. Journal of Heredity, 71:290-292.
Hauptli, H., Jain, S.B. (1984). Genetic structure of landrace populations of New World grain amaranths. Euphytica, 33:875-884.
Holovyn, V.P., Nedylko, B.A. (1995). Priemy selekczii i stimulyaczii produktivnosti amaranta. Persha Vseukr. konf. Po problemi vyroshchuvannia, pererobky i vykorystannia amaranta na kormovi, kharchovi i inshi tsili. Vinnytsia (in Ukrainian).
Hudym, O.V., Goptsiy, T.I. (2015). Indukovana minlyvist morfolohichnykh oznak u roslyn amaranta pry vykorystanni hamma-oprominennia. Visn. KhNAU. Kharkiv. Vyp, 2:45-50 (in Ukrainian).
Hudym, O.V. (2014). Vplyv mutahennykh chynnykiv na skhozhist, vyzhyvanist, rist i rozvytok roslyn amaranta. Visn. KhNAU. Kharkiv, 2:62-67 (in Ukrainian).
Hudym, O.V., Vasko, V.O., Kyrychenko, V.V., Goptsiy, T.I. (2016). Minlyvist morfolohichnykh oznak roslyn pid vplyvom hamma-promeniv. Visn. KhNAU. Kharkiv, 1:133-140 (in Ukrainian).
International Union for the protection of New Varieties of plants. (2008). Geneva, р:29.
Kapravyi, V.V. (1997). Stvorennia vykhidnoho materialu dlia selektsii amaranta zernovoho v umovakh Lisostepu Ukrainy. Thesis of Doctoral Dissertation Kyiv (in Ukrainian).
Kozachenko, M.R. (2010). Eksperymentalnyi mutahenez v selektsii yachmeniu. Kharkiv (in Ukrainian).
Morgun, V.V., Logvinenko, V.F. (1995). Mutatsionnaya selektsiya pshenitsyi. Kiev: Naukova dumka (in Russian).
Muller, H.J. (1927). Artifical transmutation of the gene. Science, 66:84-87.
Nadson, G.A. (1920). O deystvii radiya na drozhzhevyie gribki v svyazi obschey problemoy vliyaniya radiya na zhivyie veschestva. Vestnyk renthenolohyy y radyolohyy, 12:45-137 (in Russian).
Sapegin, A.A. (1935). Trudyi po prikladnoy botanike, genetike i selektsii. Moscow: VASHNIL (in Russian).
Stadler, L.J. (1928). Genetic effects of X-rays in maize. Proceedings Natural Academic Science, 14:16.
Vasko, V.O., Hudym, O.V., Rozhak, O.H. (2015). Zastosuvannia eksperymentalnoho mutahenezu v selektsii roslyn. Selektsiia i nasinnytstvo: mizhvid. temat. nauk. Zb, 107:8-18 (in Ukrainian).
Vasylkivskyi, S.P., Kunakh, V.A. (Red.). (2012). Indukovanyi mutahenez v selektsii roslyn. Bila Tserkva: BNAU (in Ukrainian).
Author Info
O.V. Hudym, S.V. Lymanska, T.I. Goptsiy, N.P. Turchynova, V.O. Mykhailenko, R.V. Kryvoruchenko, R.V. Rozhkov and S.V. Stankevych*Citation: O.V. Hudym , S.V. Lymanska , T.I. Goptsiy , N.P. Turchynova , V.O. Mykhailenko , R.V. Kryvoruchenko , R.V. Rozhkov, S.V. Stankevych (2021). Amaranth variability at different doses of gamma radiation. Ukrainian Journal of Ecology, 11 (8), 146-151.
Received: 28-Sep-2021 Accepted: 22-Oct-2021 Published: 25-Oct-2021
Copyright: This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
