Research - (2021) Volume 11, Issue 3
Abstract
The goal of this paper is to study the applicability of the conceptual model to simulate and predicting the small river flow hydrographs and maximum water discharges produced by meteorological factors in the context of climate change and land use modifications. Three small rivers, tributaries of Ob (the Bolshoy Tatosh River at the Bolshoy Tatosh gauge station) and Tom (the Basandayka River at Basandayka and the Poros River at Zorkaltsevo) are studied by means of flow hydrograph modeling based on the HBV-light model. The study area in the city of Tomsk and its vicinity is considered as a zone of compound extremes of flooding. Initial information for flow modeling includes open data of hydrometeorological observations for 2008-2017. Results of flow hydrograph simulation are of a good quality and might be useful for flow prediction in unaffected catchments, monitoring and management of flood situation in the Tomsk area and similar regions.
Keywords
Compound extremes, flood, small rivers, hydrograph simulation.
Introduction
Floods are the most important and hazardous events taking into account of their magnitude and consequences in the life of Siberian rivers (Taratunin, 2008; Zemtsov et al., 2014). In the city of Tomsk and its vicinity, people almost every year deal with ‘compound extremes’, that is, ‘the simultaneous or sequential occurrence of multiple extremes at single or multiple locations’ (Hao et al., 2018, p.1). Especially hazardous is the flood situation that includes the following dangerous processes: (1) floods in the large river of Tom, associated with a rapid increase in its water flows due to intensive snow melt and rainfalls in the river basin; (2) floods in the city and its environs, arising from ice jams, the frequency of which tends to increase (jams can also occur in years with relatively low flood water flow; they often lead to the most dangerous rises in water level and flooding in the Tom valley); (3) floods with probable destruction of river banks in small tributaries of Tom; (4) the rise in groundwater levels in the city and its environs due to abundant atmospheric precipitation and (5) dangerous hydrogenic processes, such as landslides (Matsuyama et al., 2021) on steep slopes of river valleys.
Taken together, all of the above determines the complexity of the flood situation, which should be predicted in advance, and adequate measures should be taken to reduce risks and eliminate the consequences of floods.
The goal of this paper is to study the applicability of the internationally recognized conceptual HBV light model for simulating and predict small river flow hydrographs and maximum water discharges produced by meteorological factors in the context of climate change and land use modifications. In this regard, our recent experiments in hydrographs and daily maximum water flows modeling for Arctic rivers of western Siberia based on the HBV-light model have shown encouraging results (Kopysov et al., 2020).
Study Area
The study area (Fig. 1) is located in the middle course of the Ob River, within the southeastern part of the Tomsk administrative region, around the city of Tomsk. Ob is the third largest northward flowing river in Siberia with headwaters in the Altai and Sayan Mountains. Tomsk is situated on the Tom River, the largest right tributary of the Ob. A transitional position of the study area between the mountain structures of Altai and Sayan and the west Siberian Lowland predetermines a complicated combination of hills and lowlands in the region.
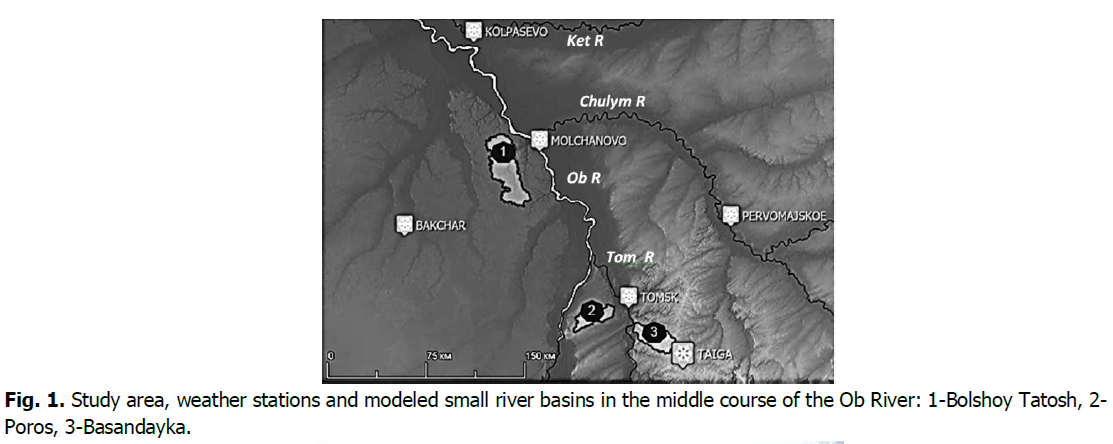
Fig 1: Study area, weather stations and modeled small river basins in the middle course of the Ob River: 1-Bolshoy Tatosh, 2-Poros, 3-Basandayka.
The rivers in the area are characteristic of a high snowmelt flood and summer to autumn rain floods; a winter low flow period when the rivers are covered by ice lasts about six months. Maximum water levels are usually produced by a passage of peak spring-summer flood flow peak water discharges. The most common are snow melt floods that occur every year during spring (in medium size and small rivers, or spring to summer high water in large rivers. The flood flow hydrograph of the Tom River in Tomsk have several peaks, produced in different landscapes of its watershed basin.
Climate warming accelerates snowmelt in the headwaters of large rivers Ob and Tom rivers that run north from the mountains. In spring, melt water quickly destroys the winter ice pack in the river channel, and ice-jam-induced floods are becoming more frequent in transition areas between hills and lowlands. During spring floods, in river mouth areas of the tributary lowland rivers backwater effects occur (Fig. 2), significantly worsening the drainage conditions of the watershed areas, increasing groundwater levels, and inducing destructive processes in the river valleys (Zemtsov et al. 2014).

Fig 2: Backwater in the Ushayka river mouth at the Tomsk city center during a snow-melt-driven flood, dammed by the ice jam at the large river of Tom in the end of April, 2010 (Territorial Center, 2020).
We study three small rivers (Table 1) that flow into the large rivers of Ob (the Bolshoy Tatosh River at the Bolshoy Tatosh gauge station) and Tom (the Basandayka River at Basandayka and the Poros River at Zorkaltsevo). Despite geographical proximity, the physiographical characteristics of these catchments, including the water flow rate and regime, are quite different and influenced by anthropogenic activities. As a result, the water budget of such small catchments is also different (Savichev et al., 2010).
| River-Gauge Station | Catch- ment Area, km2 |
Weather Stations | Catchment Center Coordinates | Calibration Period | Coefficient of Determination R2 | Model Efficiency Reff | Efficiency of Flood Flows Estimation Reff_flood |
|---|---|---|---|---|---|---|---|
| Bolshoy. Tatosh- Bol. Tatosh | 1140 | Kolpashevo, Bakchar | 57°29ˈ N 83°21ˈ E |
2008-2017 | 0.89 | 0.82 | 0.88 |
| Poros-Zorkaltsevo | 316 | Tomsk | 56°28ˈ N 84°32ˈ E |
2011-2016 | 0.80 | 0.76 | 0.91 |
| Basandayka- Basandayka | 402 | Tomsk, Taiga | 56°20ˈ N 85°11ˈ E |
2012-2018 | 0.89 | 0.89 | 0.92 |
Table 1. Localities of the gauge stations and accuracy of the flow hydrograph simulation using the HBV-light model.
Materials and Methods
For modeling river flow hydrographs with daily resolution, we apply rather simple conceptual semidistributed reservoir-type models, such as the HBV-light model (Seibert and Vis, 2012), one of new versions of the HBV model developed in the Swedish Meteorological and Hydrological Institute (Bergstrem and Forman, 1973), and the Tank Model (Sugawara et al., 1995) developed in the National Research Center for Disaster Prevention in Tokyo, Japan. After appropriate testing procedures, both the HBV and the tank model were recommended for practical use by the Hydrological Operational Multipurpose System (HOMS) established at the World Meteorological Organization for the transfer of technology in hydrology and water resources (Guide, 2009).
The HBV-light contains (1) snow routine, (2) soil moisture routine, (3) response function, and (4) routing routine (Seibert, 2005). Simulating flow hydrographs in the model with daily resolution consists of initial data preparation and selection (calibration) of the model parameters that allow calculation of the daily runoff depth based on daily air temperature and precipitation at the nearest weather stations. We carried out the parameter calibration by using manual trial and error technique as recommended in (Seibert, 2005).
Initial data for flow modeling, namely, daily precipitation, daily air temperature data for the Roshydromet period 2008 to 2017 at the weather stations of Roshydromet nearest to the modeled river basins, were taken from databases of the All-Russia Research Institute of Hydrometeorological Information-World Data Center (RIHMI-WDC) (http://meteo.ru/data). Daily river water discharges at river gauge stations used in the study were obtained from the Automated Information System for State Monitoring of Water Bodies (https://gmvo.skniivh.ru/).
Results and Discussion
The results of the river flow modeling are shown in Table 1-3. All criteria that evaluate the fit of the simulated daily water discharges to the observed flows are high (Table 1). The best fit quality was obtained for 2015 with the greatest water flow rates from the watershed areas of the study catchments (Table 2). In Table 3, calibrated values of the parameters of the HBV light model parameters are presented. Different values of the same parameter are characteristic for different study basins.
| River-Gauge Station | Catch-ment Area, km2 |
Weather Stations | Catchment Center Coordinates | Calibration Period | Coefficient of Determination R2 | Model Efficiency Reff | Efficiency of Flood Flows Estimation Reff_flood |
|---|---|---|---|---|---|---|---|
| Bolshoy. Tatosh- Bol. Tatosh | 1140 | Kolpashevo, Bakchar | 57°29ˈ N 83°21ˈ E |
2008-2017 | 0.89 | 0.82 | 0.88 |
| Poros-Zorkaltsevo | 316 | Tomsk | 56°28ˈ N 84°32ˈ E |
2011-2016 | 0.80 | 0.76 | 0.91 |
| Basandayka-Basandayka | 402 | Tomsk, Taiga | 56°20ˈ N 85°11ˈ E |
2012-2018 | 0.89 | 0.89 | 0.92 |
Table 2. Accuracy of the 2015 maximum floodwater discharge estimation using the HBV-light model.
| Parameter | Notation | Unit | Bolshoy Tatosh-Bolshoy Tatosh | Poros-Zorkaltsevo | Basandaik-Basandaika |
|---|---|---|---|---|---|
| Threshold temperature between snow and rain | TT | ºC | 2.3 | 1.5 | 0.5 |
| Degree-day factor | CFMAX | mm oC-1 day-1 |
1.3 | 1.05 | 2.8 |
| Correction factor for snow | SFCF | - | 1 | 0.8 | 1 |
| Refreezing coefficient | CFR | - | 0.05 | 0.05 | 0.05 |
| Proportion of melt water in snow pack | CWH | - | 0.1 | 0.1 | 0.1 |
| Maximum soil moisture storage | FC | mm | 120 | 300 | 380 |
| Threshold value of soil moisture | LP | - | 0.2 | 0.4 | 0.1 |
| Parameter, determining the relative contribution to runoff from rain or snowmelt |
Beta | - | 0.99 | 1.5 | 0.7 |
| Recession coefficient | K0 | day-1 | 0.4 | 0.4 | 0.1 |
| Recession coefficient for upper reservoir |
K1 | day-1 | 0.1 | 0.1 | 0.1 |
| Recession coefficient for lower reservoir |
K2 | day-1 | 0.09 | 0.09 | 0.009 |
| Storage in upper zone | UZL | mm | 35 | 15 | 20 |
| Max. percolation to lower zone | PERC | mm day-1 | 2 | 0.3 | 0.5 |
| Parameter of transformation function | MAXBAS | day | 5 | 5 | 2 |
Table 3. Values of calibrated parameters of HBV-light for maximum daily specific discharge simulation.
The most severe flood situation was observed in spring 2010. At the end of April 2010, there was a coincidence in time of three characteristic flood events (Sidorenko and Romantsov, 2010): (1) intense flood in small rivers (Ushayka, Basandayka), (2) powerful ice drift with the formation of ice-jams and dams in the river of Tom near Tomsk, and (3) rapid rise in the Tom water level due to hot weather in the Tom river basin. Usually, the time interval between these separate consecutive events in ordinary years reaches up to one to two weeks. The water level in the Tom River near the Basandayka mouth has risen by more than 2 m, the flow of the Basandayka has actually stopped, and a vast backwater zone has formed in the small river channel. ‘Observed’ water discharges were more than twice overestimated due to the calculation of Qobs using its dependence on the water level, constructed for natural conditions, without the backwater effect (Fig. 3). It was proven that the situation in 2010 was favorable for the formation of landslides due to the high intensity of snow melting and atmospheric precipitation (Matsuyama et al., 2021).
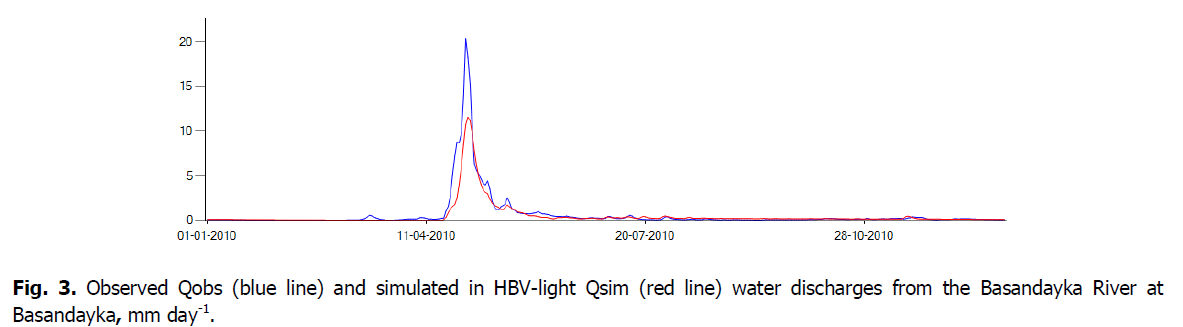
Fig 3: Observed Qobs (blue line) and simulated in HBV-light Qsim (red line) water discharges from the Basandayka River at Basandayka, mm day-1.
Conclusion
The results of the study show that the conceptual HBV light model is applicable to simulate and predicting the small river flow hydrographs and maximum water discharges produced by meteorological factors in the context of climate change and land use modifications. Important advances of the model are its ability to reproduce flow hydrographs of ungauged small rivers using only observational data from the nearest weather stations and landscape characteristics of watershed areas. The results of our study also show that the calibrated values of the model parameters differ considerably differ for different small catchments within the study area. This fact complicates the determination of model parameters for small ungauged catchments. However, the model might be useful for reconstructing/correcting time series of hydrological observations containing missing (or rejected) values such as at Basandayka gauge station (or Poros at Zorkaltsevo) in April-May 2010. In general, the results of the flow hydrograph simulation are of good quality and might be useful for the prediction of flow prediction in ungauged basins, monitoring and management of flood situations in the Tomsk area and other regions.
Acknowledgements
Financial support for this study has been provided by the Russian Federal Target Program Grant RFMEFI61419X0002. H. Matsuyama was supported by the JST/SICORP Grant Number JPMJSC1901 (Japan).
References
Automated information system for state monitoring of water bodies. Retrieved from: https://gmvo.skniivh.ru/
Bergström, S., Forsman, A. (1973). Development of a conceptual deterministic rainfall-runoff model. Nordic Hydrology, 4:147-70. Databases of Research Institute of Hydrometeorological Information-World Data Center (RIHMII-WDC). (1978).
Guide to Hydrological Practices. (2009). Management of water resources and Applications of hydrological practices, WMO No. 168. Hao, Z., Singh, V.P., Hao, F. (2018). Compound extremes in hydroclimatology: A review. Water, 10:718.
Kopysov, S.G., Zemtsov, V.A., Matsuyama, H., Eliseev, А.O. (2020). River flow hydrograph simulation in the Western Siberia Lowland north for the extreme flood flow prediction based on the HBV-light model. Geosphere Research, 2020:108-120.
Matsuyama, H., Saito, H., Zemtsov, V. (2021). Application of the soil water index to landslide prediction in snowy regions: sensitivity analysis in Japan and preliminary results from Tomsk, Russia. Progress in Earth and Planetary Science.
Savichev, O.G., Bolom, I., Kharanzhevskaya, Y.A. (2010). Long-term changes of the water balance elements in the small river basins in the south of Western Siberia. Bulletin of Tomsk Polytechnic University, 316:124-128.
Seibert, J. (2005). HBV light version 2. User’s Manual. Stockholm, Sweden:Stockholm University.
Seibert, J., Vis, M.J.P. (2012). Teaching hydrological modeling with a user-friendly catchment-runoff-model software package. Hydrology Earth Systems and Science, 16:3315-3325.
Sidorenko, S.V., Romantsov, A.D. (2010). Satellite monitoring of the tom river flash flood. Zemlya iz Kosmosa, 6:70-77 (in Russian). Sugawara, M. (1995). Tank model. In: V.P. Singh (Ed.), Computer models of watershed hydrology. Highlands Ranch, Colorado, USA: Water Resources Publications.
Taratunin, A.A. (2008). Floods in the Russian Federation. Yekaterinburg, Russia: RosNIIVH Publishing (in Russian). Territorial Center ‘Tomskgeomonitoring’. (2020). Tomsk. Retrieved from: https://www.tgm.ru/.
Zemtsov, V.A., Paromov, V.V., Kopysov, S.G., Kouraev, A.V., Negrul, S.V. (2014). Hydrological risks in Western Siberia under the changing climate and anthropogenic influences conditions. International Journal of Environmental Studies, 71:611-617.
Author Info
V.A. Zemtsov1*, S.G. Kopysov1, H. Matsuyama2 and S.V. Negrul12Tokyo Metropolitan University, Tokyo, Japan
Citation: Zemtsov, V.A., Kopysov, S.G., Matsuyama, H., Negrul, S.V. (2021). River flow hydrograph simulation using the HBV-light model (an example of small rivers in Tomsk city, Western Siberia, Russia). Ukrainian Journal of Ecology, 11 (3), 406-409.
Received: 09-May-2021 Accepted: 10-Jul-2021 Published: 24-Sep-2021, DOI: 10.15421/2021_0190
Copyright: This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
