Review - (2022) Volume 12, Issue 5
Using the CFD capabilities of FDS to predict a vegetation fire in a sloped terrain
A. Soummar and H. Miloua*Abstract
The Fire Dynamics Simulator (FDS) developed by the National Institute of Standards and Technology (NIST) is a computational fluid dynamics (CFD) model of fire-driven fluid flow using a large-eddy simulation (LES) turbulence model for low-speed flows, with an emphasis on smoke and heat transport from fires. Smokeview is a program used to visualize numerical calculations generated from FDS. The validation and verification of the proposed fire models (FDS) for vegetation fire data at laboratory-scale experiments is the subject of this paper by comparing the fire front positions values and thermal functions such as the heat release rate (HRR) measured by Moredirini et al. (2018) from spreading fires for fuel bed slopes of 0° and 30° tested under two fuel loads of 0.6 and 0.4 kg.m-2,with no wind imposed. The results can be useful for the improvement and validation of FDS and provide global information on forest fire propagation under no slope and upslope terrain. The convergence of measured and predicted fire front position values is quite good, demonstrating that FDS accurately described plate and sloped fire.
Keywords
FDS, Fire, HRR, Slope, Validation, Vegetation.
Nomenclature
Variable Description, Units
Cpmix: Specific heat for mixture.
G(r;Δ): Filter kernel of characteristic width Δ,m-3
h=ΣiYihi: Mixture enthalpy, kJ kg-1
hi: Specific enthalpy of species i, kJkg-1
I: Identity matrix
I(x, 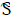 ): Radiation intensity, W MHz m-2sr-1
): Radiation intensity, W MHz m-2sr-1
Ib(x, 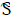 ): Blackbody radiation intensity, W MHz m-2sr-1
): Blackbody radiation intensity, W MHz m-2sr-1
J: Diffusive mass flux, kg m-2s
k: Thermal conductivity, W m-1K-1
m: Mass, kg
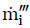 : Chemical mass consumption of gas species i, kg m-3s-1
: Chemical mass consumption of gas species i, kg m-3s-1
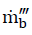 : Mass production due to thermal degradation of vegetation, kg m-3s-1
: Mass production due to thermal degradation of vegetation, kg m-3s-1
Mmix: Mass flow rate of the chemical compounds-air mixture determined from the volumetric flow rate of the mixture through the duct.
N: Number of fuel elements
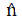 : Unit normal vector
: Unit normal vector
p: Hydrodynamic pressure, Pa
p0: Thermodynamic pressure, Pa
q: Heat flux vector, kW m-2
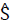 : Unit vector in direction of radiation intensity
: Unit vector in direction of radiation intensity
T: Gas temperature,°C
u: Velocity vector, m s-1
V: Volume, m3
xrad: Radiant fraction of the flame
xconv: Convective fraction
x: Position vector, m
Yi=ρi⁄ρ Mass fraction of species i
S: Surface area, m2
Δx;Δy;Δz: Grid spacing, m
δ(x): Dirac delta function, m-3
k: Radiative absorption coefficient
μ: Dynamic viscosity of the gaseous mixture, kg m-1s-1
ρ: Mass density, kg m-3
τ: Stress tensor, Pa
Subscripts
a: Ambient
b: Bulk vegetative fuel quantity or blackbody
e: Fuel element type
i: Gaseous species
k: Fuel element index
r: Radiative
t: Turbulent
Superscripts
d: Deviatoric part
sgs: Subgrid scale
Special operators

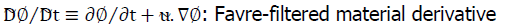
Introduction
Wildfires are a phenomenon that may be characterized by a high level of destruction of material and human property. The slope of the terrain is one of the most critical factors in wildfire propagation, generally because of its strong influence on the fire front's rate of spread (Fons, W. L.,1946; Linn, R et al.,2007). The slope of the terrain is generally recognized as a key consideration in controlling the spread of wildfires. The impacts of terrain slope have been included in wildfire modeling methods for decades. The increase in the rate of spread is often explained by the fact that the flames are closer to or in direct contact with the vegetation, but the reality is that the general dynamics of the flame and the induced flow are subject to much more essential changes (Dold, J. W., and Zinoviev, A.,2009; Morandini, F et al.,2014). In overall, the slope does have a big impact on flame geometry, and it plays a big part in how fast the fire spreads and how much heat it transfers (Dupuy et al.,2011; Finney, M. A et al.,2011; Silvani, X. et al.,2012). It has long been known that the slope of the terrain plays a key role in the spread of wildfires (Hawley, L. F., 1926; Silvani, X. et al., 2012). Positive slopes (upslopes) often result in a higher rate of spread, whereas negative slopes (downslopes) result in a lower rate of spread than the level ground rate of spread. Particular attention should be paid to the heat transfer processes that govern the spread of forest fires, particularly convection, which has received less attention than radiation (Yedinak, K. M et al., 2010; Finney, M. A et al., 2012). However, the radiation from the flame alone cannot fully explain the spread of fire through the vegetative fuels, which should instead be caused by a heat transfer between radiative and convective [Dupuy, J. L et al.,2011; Yedinak, K. M et al.,2010; Anderson, W. R.,2010). For example, in pine-needle fuel beds, laboratory experiments aimed at exploring the roles of radiation and convection heat transfer for different slopes were conducted. When the slope angle is between 0° and 20°, radiative heat transmission dominates, but when the slope angle is extended to 31°, convective heat transfer takes over. Morandini, F., and Silvani, X. (2010) achieved similar results in their field studies. Morandini et al. (2014) and Grumstrup (2017) looked into why the function of convective heat transfer rises as the slope increases, concentrating on flow around the flame base and the prevalence of flame attachment.
Physical-based models of different types were used to explore the influence of topography, wind and fuel bed on fire propagation (Linn, R et al.,2007; Morandini, F et al.,2001; Linn, R et al.,2010). To evaluate laboratory ROS under different slope and wind situation, Morandini et al. (Morandini, F et al.,2001) employed a non-CFD technique, a model based on radiation heat transfer. Find the right chord for slope angles from 0° to 20°. Considering the increasing tendency of using computer simulation to estimate fire propagation edges, developments in three-dimensional information systems on topography have made bushfire spread calculations easier (Dupuy, J. L., and Morvan, D. 2005; Finney, M. A. 1998). More research on the fundamentals of flow aerodynamics, exposing the effects of ground slope on fire-wind improvement behavior, is always required. R. Linn et al., 2007). The possibility that slope effects are dependent upon the structure of the fuel bed was also analyzed using FIRETEC (Linn, R et al., 2010).
The model used here is physics-based and employs computational fluid dynamics (CFD) approaches to depict both the heat release rate from burned vegetation and heat transfer modes transfer by conduction, radiation, and convection, and it may be used to help us better understand the physical mechanisms that govern vegetation fire behavior at the laboratory scale.
Materials and Methods
Experiment description
The data of was collected in June 2014 on the DESIRE bench at the INRA facility in France through a series of ten fire spread experiments of Morandini et al. (2018). Fig. 1 depicts the entire experimental pattern schematically. This laboratory bench is 10 meters long and 4 meters wide, with a tiltable plate made of insulating material (ventilated concrete, Siporex). The bench is housed in a 20-meter-long, 12-meter-wide, and 12-meter-high experimental hall with a passive fume and heat exhaust system (large roof ventilation openings).
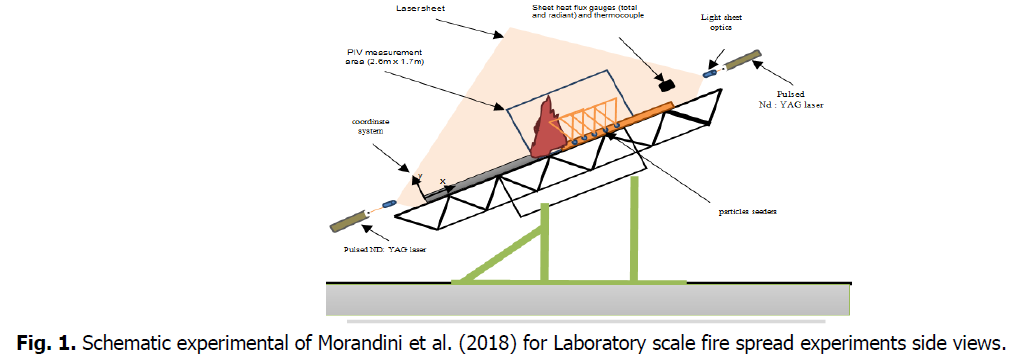
Fig 1: Schematic experimental of Morandini et al. (2018) for Laboratory scale fire spread experiments side views.
The fuel was a 7-meter-long, 3-meter-wide bed of excelsior. Fuel loadings of 0.2, 0.4, and 0.6 kg/m2 were investigated. The fuel had a surface-to-volume ratio of 4730 m-1 and a density of 1.3 g/cm3. The fuel was a 7-meter-long, 3-meter-wide bed of excelsior. Fuel loadings of 0.2, 0.4, and 0.6 kg/m2 were investigated. The fuel's surface-to-volume ratio was 4730 m-1, and its density was 780 kg/m3. Prior to the fire test, the fuel had not been conditioned, and the moisture content was around 10%. Morandini et al. (2018) used 20 mL of alcohol to start a fire line at one end of the bench in their experiment.
CFD code and used mathematical models
FDS aims to solve the governing equations for buoyant flow, combustion (i.e., heat release), heat transmission (Mell, W et al., 2013), and the thermal degradation of vegetative fuels using approximation equations.The governing equations (Eq. 4-8) must be deduced, and particular numerical approaches such as large eddy simulation (LES) must be utilized to a coherent convergence to the reality so that acceptable applicability boundaries and numerical parameters may be established through validation studies.
A low-pass spatial filtering process in LES explicitly defines the "large" (i.e., resolved) and "small" (i.e., subgrid) scales. We distinguish between two types of filtering used to generate the governing equations for an arbitrary scalar: conventional filtering and explicit filtering. In the simulation, conventional LES quantities are implicitly filtered. Explicit filtering, according to Pope 2000, employs an anisotropic box filter to find the bulk source terms owing to the presence of subgrid fuel components. A conventional filter with the Heavyside kernel is applied to obtain:
The distinct drag sources are explicitly filtered, resulting in (Mell, W et al.,2007; Susott, R. A. 1982).
The value of the drag factor tested under "CD" is dependent on the local Reynolds number, Ree
The filtered mass, species, momentum, and enthalpy transfer equations, coupled with EOS (the equation of state), as demonstrated in Eqs. (4)–(7), write ns+ 5 independent equations for ns+5 unknowns: density, ns-1 mass fractions, 3 velocity components, hydrodynamic pressure, and enthalpy (ns is the number of species).
The filtered material derivative D̃D̃t⁄ is applied to the filtered EOS in the LES context, producing in
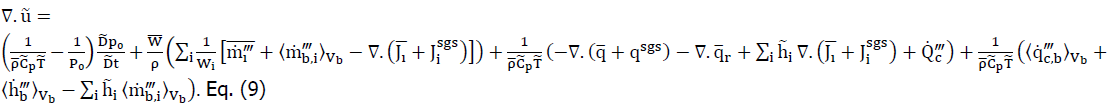
This constraint is employed in the Poisson equation for hydrodynamic pressure (derived from the divergence of the momentum equation). Note that the following relationships are utilized to produce the following results (which are not obtained by applying the filter operators in a straight-forward manner).
Molecular coefficients are assessed using filtered temperature and species concentrations to yield Favre-filtered transport coefficients, 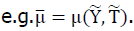 The constant coefficient Smagorinsky model is used to calculate the eddy viscosity,
The constant coefficient Smagorinsky model is used to calculate the eddy viscosity, 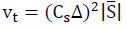 with Cs=0.2 and Δ= Vb1/3. The strain rate's magnitude, is
with Cs=0.2 and Δ= Vb1/3. The strain rate's magnitude, is 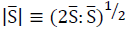 . The turbulent Schmidt and Prandtl numbers are set to SCt=0.5 and Prt=0.5, respectively, based on comparisons between FDS and compartment fire experiments (Morvan, D., and Dupuy, J. L.,2001; Morvan, D., and Dupuy, J. L.,2004).
. The turbulent Schmidt and Prandtl numbers are set to SCt=0.5 and Prt=0.5, respectively, based on comparisons between FDS and compartment fire experiments (Morvan, D., and Dupuy, J. L.,2001; Morvan, D., and Dupuy, J. L.,2004).
The rate of heat release from combustion may be calculated using mixture fractions or the Eddy Dissipation Concept (EDC) model, which has been discussed in several studies (Magnussen, B. F., and Hjertager, B. H.,1977, January; Miloua, H.,2016; Miloua, H et al.,2011).
FDS has gotten a lot of interest because it can forecast fire behavior in more detail under a variety of scenarios than other commonly used models (Mell, W et al.,2013). WFDS is a three-dimensional physics-based computational fire model capable of predicting fine-scale time-dependent fire behavior, as well as fire–fuel and fire–atmosphere interactions (Mell, W et al.,2013), Including physical processes with less heuristic physically driven assumptions. The thermal deterioration of a solid fuel, for example, is exclusively determined by the resolved net heat flow on the fuel. In the gas-phase calculation, the equations solved and numerical approach utilized are substantially the same as those used by McGrattan (2004). The gas phase sees vegetation as a source of momentum drag, heat, and mass fluxes at the gas phase's bottom boundary. The top edge of the grid for the vegetative fuel bed has both heat flux (from the fire) and fuel gas flux (from pyrolysis). The approach solves the gas-phase equations using computational grids that are too coarse to directly resolve the precise physical events using large eddy simulation (LES) techniques.
Due to the thermal depreciation of the kth subgrid fuel element, the discrete mass source for gas species i is
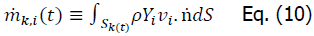
The discrete mass source density can therefore be defined as
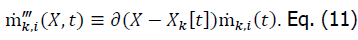
We get the bulk discrete mass source density by summing Eq. (2) across all fuel components.
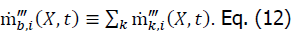
In addition, adding up the gas species yields
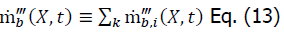
Computational domain and conditions
Morandini et al. (2010) conducted a laboratory-scale grass vegetation experiment devoted to the experimental characterization of the processes involved in upslope fire spread. The same dimensions and conditions (Fig. 1) were reproduced for the computational domain (Fig. 2) with 7 × 3 × 3 m, considered for this study. Different fuel loads (w) were tested, such as 0.6 and 0.4 kg.m-2. Fig. 2 shows an overview of this domain and the fuel bed with no-sploe and 30° up-slope. It is displayed by the Smokeview visualization package (Forney, G.P., 2017).
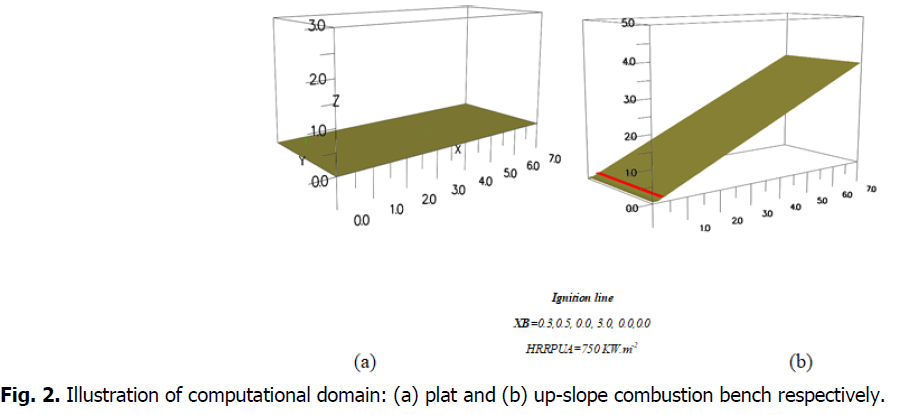
Fig 2: Illustration of computational domain: (a) plat and (b) up-slope combustion bench respectively.
In our simulations, a set amount of heat release rate per unit area (HRRPUA) emitted throughout a few seconds ensures the ignition line at the inlet (XB=0.3,0.5, 0.0, 3.0, 0.0, 0.0). Concerning boundary conditions, the inlet and outlet are open like two faces on top. For scalar fields, zero gradient boundary conditions are utilized on the open limits of the computational domain; velocity and pressure boundary conditions are more involved and are described in Mc Grattan et al. (2013). The ground is assumed to be vegetation. whereas there is no loss of heat to the soil and it is presumed adiabatic. The model's mass loss rate and radiant heat flow estimates were investigated for sensitivity to grid resolution and computational domain size. The simulations are run on an Intel(R) Core(TM) i7-8565U CPU running at 1.80GHz and 1.99GHz with 16GB of RAM.
The slope values cases are given in Table 1 with the corresponding values of w used in the simulation.
The numerical domain height was set to 3 m and 5 m with a no-slope and up-slope of 30° respectively, for the simulated experimental instances listed in Table 1 in order to achieve the maximum flame height of the experimental cases. Morandini et al. (2014) The experimental ignition procedure was modeled by using an ignition line at the inlet (XB=0.3,0.5, 0.0, 3.0, 0.0, 0.0) with HRRPUA=750 KW.m-2, This ignition line is reached in 0 s and lasts for 20 s.
The following are some of the most important thermophysical qualities that must be used as input parameters in numerical simulations:
• The fuel bed is represented as a terrain case of fuel elements. Since the two fuel loads are 0.4 and 0.6 kg.m-2
• Fuel element properties
• The surface-to-volume ratio of the fuel is 4730 m-1
• Initial temperature: taken from the condition of experience (Table 1).
• Moisture content: M=10%
• Gas phase properties: heat of combustion: hc=18850 kJ/kg-1.
| Test Scenario | Slope (degrees °) | Fuel load, (kg m2) | Fuel depth, δ (cm) | Mean moisture, m (%) | Initial temperature (C°) |
|---|---|---|---|---|---|
| 1 | 0 | 0.4 | 17 | 10 | 25.7 |
| 3 | 0 | 0.6 | 22 | 10 | 26.9 |
| 4 | 30 | 0.4 | 18 | 10 | 20.3 |
| 6 | 30 | 0.6 | 21 | 10 | 20.4 |
Table 1. Vegetation properties and numerical conditions used in FDS code.
Results and Discussion
Rate of fire spread
In this section, the ability of FDS to reproduce observed fire behavior will be evaluated by comparing it to a variety of fire behavior measures. For each scenario, flame properties were calculated at various points in time (Fig. 3). The standard deviations and mean values of these quantities are displayed. On one side of the excelsior beds, a line fire was started. When there was no slope, the fire fronts formed a curvilinear shape (like a U) during spread (Fig. 4.a). The curvature increased with the slope angle and produced a pointed shape for a slope of 30 degrees (like a V) during their spread (Fig. 4b). The fire front occasionally jumped under slope conditions (direct flame contact on distant fuel), indicating non-steady convective heating. With increasing fuel load and slope angle, the rate of spread and fire intensity rises. The extreme configuration has a higher variability in the rate of upward spread (Table 1). Under slope conditions, the properties of the flames, which are related to the released heat, show more variability.
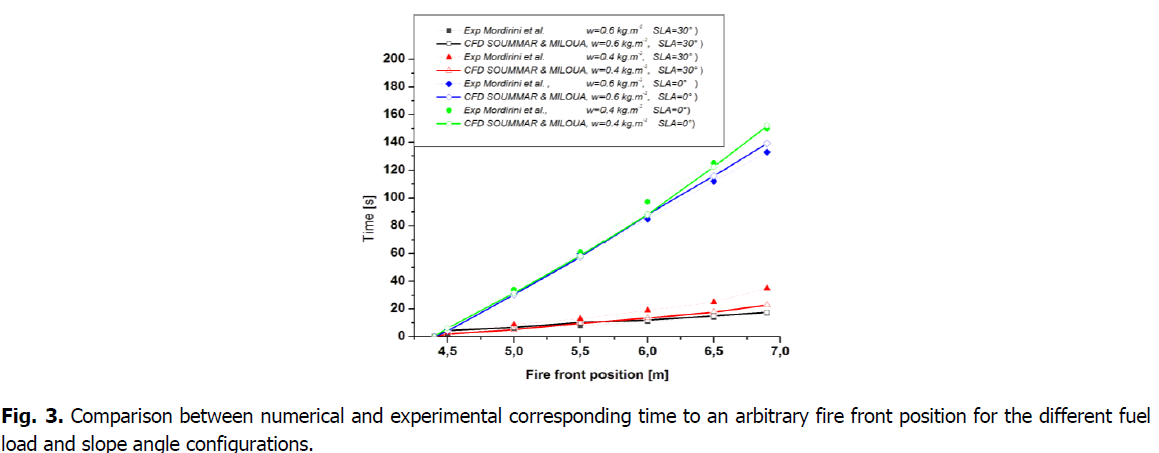
Fig 3: Comparison between numerical and experimental corresponding time to an arbitrary fire front position for the different fuel load and slope angle configurations.
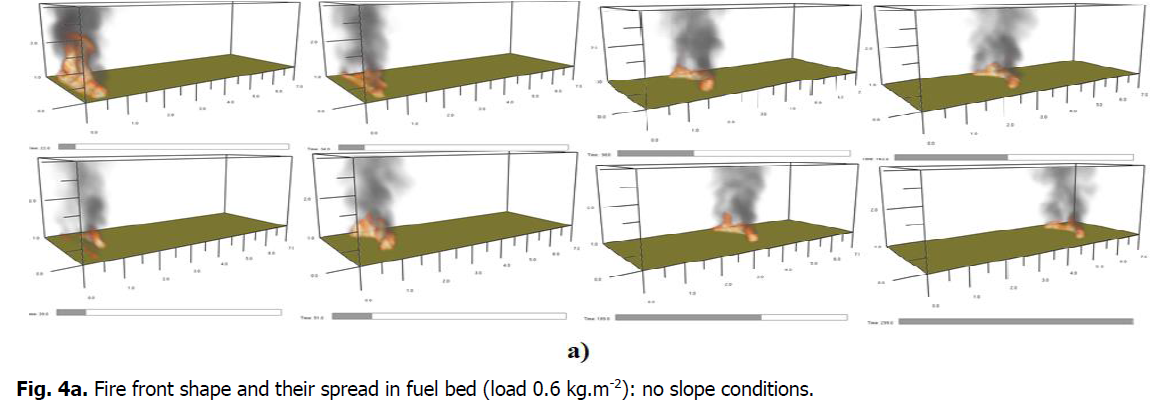
Fig 4a: Fire front shape and their spread in fuel bed (load 0.6 kg.m-2): no slope conditions.
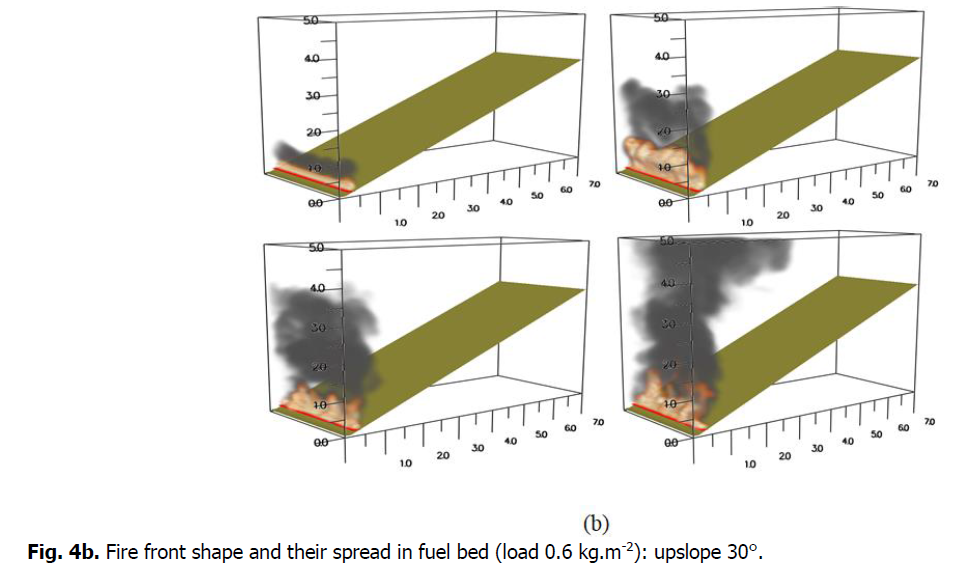
Fig 4b: Fire front shape and their spread in fuel bed (load 0.6 kg.m-2): upslope 30°.
Velocity fields
A wide range of gas velocity is involved in spreading fires, the reactive flow region has a high velocity, whereas the entrainment zone has a low velocity. Flame fronts have a virtually vertical plume under no slope condition, arising from the fire's upward buoyancy pressures. Because of the increased mass loss rate and heat release rate, the buoyancy effects and flame heights rise as the fuel load increases (Morandini, F et al., 2013). Between the intermittent flame and the smoke plume are the highest velocities. The combustion gases are accelerated upward in this area, and the velocity, maximum is close to 3 m/s for 0.6 kg/m2 fuel load in no slope scenario shown in Fig. 5.
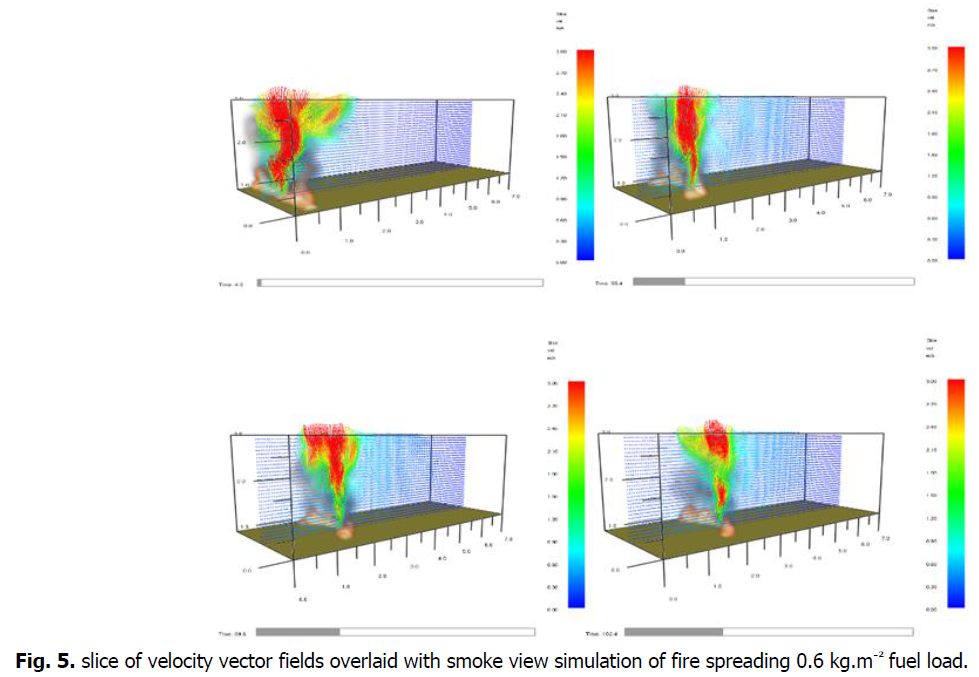
Fig 5: slice of velocity vector fields overlaid with smoke view simulation of fire spreading 0.6 kg.m-2 fuel load.
Heat Release Rate (HRR)
The heat release rate is one of the most important parameters for understanding combustion processes (HRR). Fig. 6 shows that under the same load of 0.6 kg/m2, HRR generated by fire in up-slope ground were more important than in no-slope ground. The HRR is a measurement of how much energy is released when a plant is burned, and it can change over time. In up-slope vegetation fire ground, the HRR generated by vegetation fire was twice that of no-slope values.
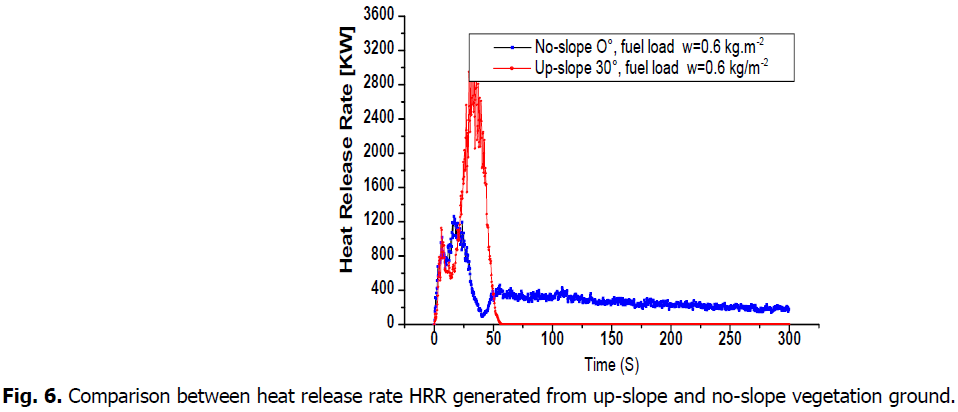
Fig 6: Comparison between heat release rate HRR generated from up-slope and no-slope vegetation ground.
Thermal functions
Q_TOTAL (KW) is the total of the terms on the right side of the equation This sum should theoretically equal the term on the left, Q_ENTHALPY. Note that the terms that make up Q_PARTICULE are summed over the Lagrangian particles. They represent the heat absorbed by the particles via convection, radiation, and conduction from the table bench. Three heat transfer modes can contribute to the mechanism of fire spread through beds of vegetation at laboratory or large scale fire: radiant, convective, and conductive heat transfer. The heat transfer processes that occur during fire spread are impacted by the slope of the terrain. Radiation heat transfer dominate over convection heat transfer in vegetation fire spread and became more with up-slope terrain (Fig. 7).
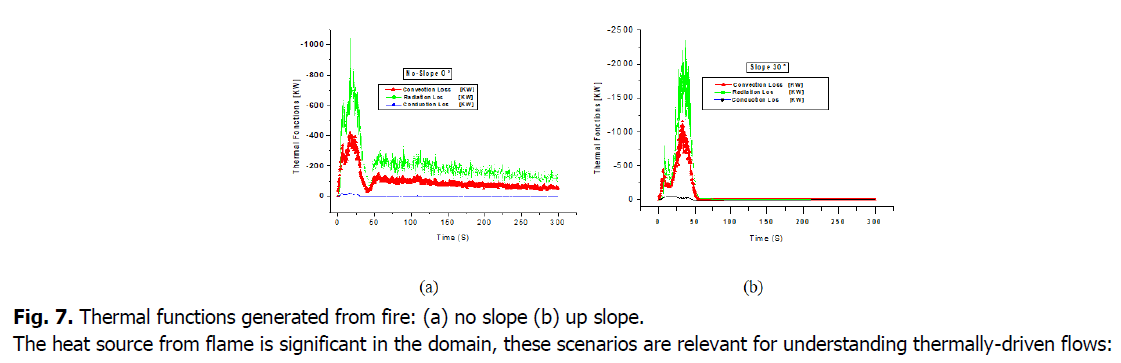
Fig 7: Thermal functions generated from fire: (a) no slope (b) up slope.
The heat source from flame is significant in the domain, these scenarios are relevant for understanding thermally-driven flows:

Conclusion
The validation of FDS with the previous experiment is presented in this study, extending the capabilities of these models, as well as improving their accuracy and reliability to model flame spread over complex surfaces and wildland terrain. The maximum values of ROS have been observed with an upslope spread. The HRR and related thermal functions have been presented for sloped and plate combustion benches. Thermal radiation was the primary heat transfer mode in the preheating zone of up-slope terrain. Based on our results, it is found that the proposed method is capable of reproducing the transient fire induced phenomenon from the experiment.
Acknowledgment
The funding was provided by Algerian Research Organism DGRSDT, under the project [No. A11N01UN020120150001].
Conflict of Interest
The authors declare they have no conflict of interest.
References
Anderson, W.R., Catchpole, E.A., Butler, B.W. (2010). Convective heat transfer in fire spread through fine fuel beds. International Journal of Wildland Fire, 19:284-298.
Dold, J.W., Zinoviev, A. (2009). Fire eruption through intensity and spread rate interaction mediated by flow attachment. Combustion Theory and Modelling, 13:763-793.
Dupuy, J.L., Morvan, D. (2005). Numerical study of a crown fire spreading toward a fuel break using a multiphase physical model. International Journal of Wildland Fire, 14(2):141-151.
Dupuy, J.L., Maréchal, J., Portier, D., Valette, J.C. (2011). The effects of slope and fuel bed width on laboratory fire behaviour. International Journal of Wildland Fire, 20:272-288.
Finney, M.A. (1998). FARSITE, Fire Area Simulator-model development and evaluation. US Department of Agriculture, Forest Service, Rocky Mountain Research Station.
Finney, M.A., McAllister, S.S. (2011). A review of fire interactions and mass fires. Journal of Combustion.
Finney, M.A., Cohen, J.D., McAllister, S.S., Jolly, W.M. (2012). On the need for a theory of wildland fire spread. International Journal of Wildland Fire, 22:25-36.
Forney, G.P. (2017). Smokeview (Version 5)-A Tool for Visualizing Fire Dynamics Simulation Data, Volume I: User's Guide.
Fons, W.L. (1946). Analysis of fire spread in light forest fuels. Journal of Agricultural Research, 72:92-121.
Grumstrup, T.P., McAllister, S.S., Finney, M.A. (2017). Qualitative flow visualization of flame attachment on slopes. In Presented at the 10th US National Combustion Meeting Organized by the Eastern States Section of the Combustion Institute; April 23-26, 2017; College Park, MD. Pittsburgh, PA: The Combustion Institute.
Hawley, L.F. (1926). Theoretical considerations regarding factors which influence forest fires. Journal of Forestry, 24:756-763.
Linn, R., Winterkamp, J., Edminster, C., Colman, J.J., Smith, W.S. (2007). Coupled influences of topography and wind on wildland fire behaviour. International Journal of Wildland Fire, 16:183-195.
Linn, R.R., Winterkamp, J.L., Weise, D.R., Edminster, C. (2010). A numerical study of slope and fuel structure effects on coupled wildfire behaviour. International Journal of Wildland Fire, 19:179-201.
Magnussen, B.F., Hjertager, B.H. (1977). On mathematical modeling of turbulent combustion with special emphasis on soot formation and combustion. In Symposium (international) on Combustion, 16:719-729.
McGrattan, K.B., Baum, H.R., Rehm, R.G., Hamins, A., Forney, G.P., Floyd, J.E., Prasad, K. (2004). Fire dynamics simulator (version 4) technical reference guide. NIST Special Publication, 1018:94.
McGrattan, K., Hostikka, S., McDermott, R., Floyd, J., Weinschenk, C., Overholt, K. (2013). Fire dynamics simulator technical reference guide volume 1: mathematical model. NIST Special Publication, 1018:175.
Mell, W., Jenkins, M.A., Gould, J., Cheney, P. (2007). A physics-based approach to modelling grassland fires. International Journal of Wildland Fire, 16:1-22.
Mell, W., Maranghides, A., McDermott, R., Manzello, S.L. (2009). Numerical simulation and experiments of burning douglas fir trees. Combustion and Flame, 156:2023-2041.
Mell, W., Charney, J., Jenkins, M.A., Cheney, P., Gould, J. (2013). Numerical simulations of grassland fire behavior from the LANL-FIRETEC and NIST-WFDS models. In Remote Sensing and Modeling Applications to Wildland Fires. Springer, Berlin, Heidelberg, pp:209-225.
Miloua, H., Azzi, A., Wang, H.Y. (2011). Evaluation of different numerical approaches for a ventilated tunnel fire. Journal of fire sciences, 29(5):403-429.
Miloua, H. (2016). Numerical prediction of the fire spread in vegetative fuels using NISTWFDS Model. In International Journal of Engineering Research in Africa. Trans Tech Publications Ltd, 20:177-192.
Morandini, F., Santoni, P.A., Balbi, J.H. (2001). The contribution of radiant heat transfer to laboratory-scale fire spread under the influences of wind and slope. Fire Safety Journal, 36:519-543.
Morandini, F., Silvani, X. (2010). Experimental investigation of the physical mechanisms governing the spread of wildfires. International Journal of Wildland Fire, 19:570-582.
Morandini, F., Perez-Ramirez, Y., Tihay, V., Santoni, P.A., Barboni, T. (2013). Radiant, convective and heat release characterization of vegetation fire. International Journal of Thermal Sciences, 70:83-91.
Morandini, F., Silvani, X., Honoré, D., Boutin, G., Susset, A., Vernet, R. (2014). Slope effects on the fluid dynamics of a fire spreading across a fuel bed: PIV measurements and OH* chemiluminescence imaging. Experiments in Fluids, 55:1-12.
Morandini, F., Silvani, X., Dupuy, J.L., Susset, A. (2018). Fire spread across a sloping fuel bed: Flame dynamics and heat transfers. Combustion and flame, 190:158-170.
Morvan, D., Dupuy, J.L. (2001). Modeling of fire spread through a forest fuel bed using a multiphase formulation. Combustion and Flame, 127:1981-1994.
Morvan, D., Dupuy, J.L. (2004). Modeling the propagation of a wildfire through a Mediterranean shrub using a multiphase formulation. Combustion and Flame, 138:199-210.
Silvani, X., Morandini, F., Dupuy, J.L. (2012). Effects of slope on fire spread observed through video images and multiple-point thermal measurements. Experimental Thermal and Fluid Science, 41:99-111.
Susott, R.A. (1982). Characterization of the thermal properties of forest fuels by combustible gas analysis. Forest Science, 28:404-420.
Yedinak, K.M., Cohen, J.D., Forthofer, J.M., Finney, M.A. (2010). An examination of flame shape related to convection heat transfer in deep-fuel beds. International Journal of Wildland Fire, 19:171-178.
Author Info
A. Soummar and H. Miloua*Citation: Soummar, A., Miloua, H. (2022). Using the CFD capabilities of FDS to predict a vegetation fire in a sloped terrain. Ukrainian Journal of Ecology. 12:47-56.
Received: 18-May-2022, Manuscript No. UJE-22-64205; , Pre QC No. P-64205; Editor assigned: 20-May-2022, Pre QC No. P-64205; Reviewed: 02-Jun-2022, QC No. Q-64205; Revised: 08-Jun-2022, Manuscript No. R-64205; Published: 15-Jun-2022, DOI: 10.15421/2022_374
Copyright: This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
